Eddington's Temperature of Space

Arthur Stanley Eddington, in the last chapter of his 1926 book The Internal Constitution of the Stars, talks about Diffuse Matter in Space. In the first page of this chapter, Eddington computes an effective temperature of 3.18 K, but this has nothing to do with the 2.725 K blackbody spectrum of the Cosmic Microwave Background (CMB). Here is a quote of what Eddington actually said:

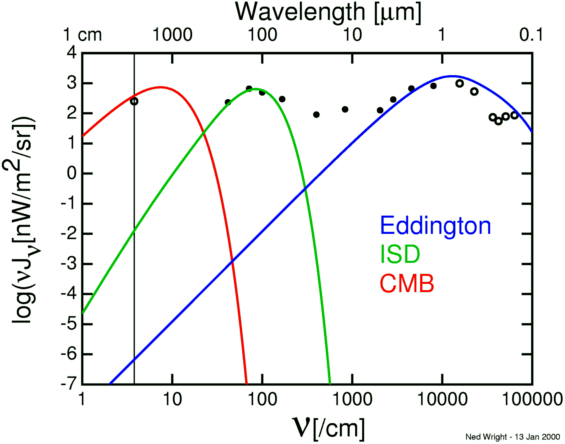
The total light received by us from the stars is estimated to be equivalent to about 1000 stars of the first magnitude. [...] We shall first calculate the energy density of this radiation. [...] Accordingly the total radiation of the stars has an energy density of [...] E = 7.67 10^-13 erg/cm³. By the formula E = a T⁴ the effective temperature corresponding to this density is 3.18^o absolute. [...] Radiation in interstellar space is about as far from thermodynamical equilibrium as it is possible to imagine, and although its density corresponds to 3.18^o it is much richer in high-frequency constituents than equilibrium radiation of that temperature.

Eddington then specifies a model for the spectrum of his estimate for the interstellar radiation field which is plotted in blue in the figure below.
$graph of nu*J_\nu vs wavelength$
It is clear that Eddington's model fits the optical data, but that Eddington did not anticipate either the CMB (red curve) or the interstellar dust (ISD, green curve). In fact, Eddington's model is a factor of more than 700 million times too small at the 2.64 mm wavelength of the CN transition [the vertical line on the left in the plot] where a measurement of 2.3 K was made in 1941. Unfortunately, this measurement by McKellar was not interpreted correctly and the CMB was not discovered until 1965.

The near equality of the energy densities of starlight (Eddington's blue curve) and the CMB is just a coincidence. The starlight radiation field is concentrated in galaxies like the Milky Way, which only occupy one part per million of the volume of the Universe, while the CMB fills the entire Universe. The diagram below shows three galaxies and the photons they emit color-coded red, green and blue.

A typical line-of-sight for observing the CMB is shown in black above. For almost all of the line-of-sight the radiation due to starlight is very small, as shown in position B. But the radiation field discussed by Eddington is within our Galaxy, as shown in position A. This is a very unusual position with a much higher radiation field than a typical location. Thus the 3.18 K effective temperature of the interstellar radiation field is no more relevant to the CMB than the 300 K effective temperature of interplanetary space near the Earth. If the solar system were opaque at the millimeter wavelengths of the CMB, we would see a 300 K blackbody; and if the Milky Way were opaque to mm waves we would see a 3.18 K blackbody; but neither the solar system nor the Milky Way is opaque. We have actually seen sources out to great distances at millimeter wavelengths, so we know the Universe is not opaque until we get back to the high temperatures and high densities that existed shortly after the Big Bang.

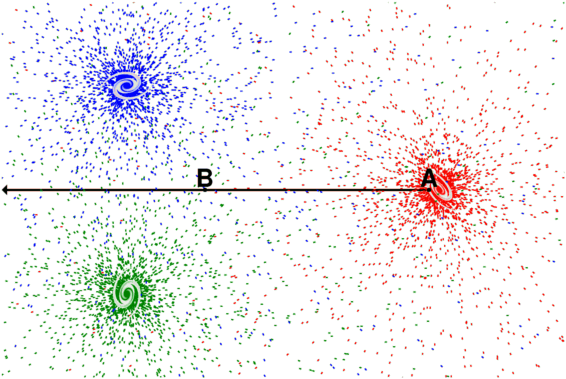
The density of radiation at position B would be relevant to the CMB if there were dust grains which could absorb this radiation and if these dust grains were able to radiate efficiently at the millimeter wavelengths of the CMB. We can estimate the radiation at B from our location at A if we carefully subtract out all the "red" photons to determine the Cosmic InfraRed [and optical] Background Radiation (CIBR). However,

The CIBR is much smaller than the CMB, so there is not enough energy.
We see galaxies at great distance in the IR, so there are not enough dust grains to absorb and reradiate the CIBR.
The dust grains in the Milky Way do not radiate efficiently at millimeter wavelengths.

Thus the effective temperature of the interstellar radiation in the Milky Way is irrelevant in cosmology and Eddington made no mention of it in his 1933 book, Expanding Universe. This book discusses Eddington's cosmological model, which starts out as the Einstein static model in which the repulsive cosmological constant just balances the gravitational attraction due to matter. But Eddington showed that this equilibrium was unstable, and the Einstein model would either collapse or start an unending expansion. Since the Universe was observed to be expanding, Eddington assumed that the initially static Universe fell out of equilibrium in the direction of expansion.